磁偶极矩

贡献者： ACertainUser

本词条处于草稿阶段．

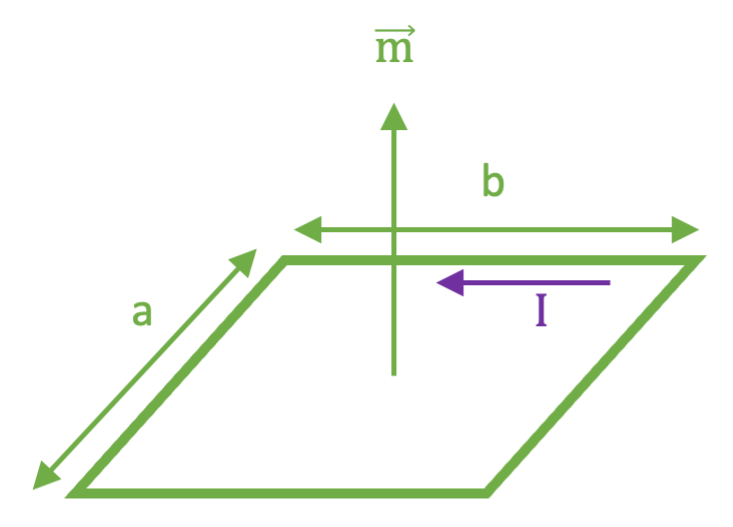
　　类似于电偶极子，我们可以定义磁偶极子．在经典电动力学中，磁偶极子可以理解为一个带恒定电流的环形小回路．

图 1：磁偶极子示意图

　　定义他的磁偶极矩 $ \boldsymbol{\mathbf{m}} $ 为

\begin{equation} \boldsymbol{\mathbf{m}} = I \boldsymbol{\mathbf{s}} \end{equation}

其中 $I$ 是这个回路的电流，$ \boldsymbol{\mathbf{s}} = ab \boldsymbol{\mathbf{n}} $ 是面积元矢量，数值上等于回路的面积，方向由电流方向与右手法则确定．

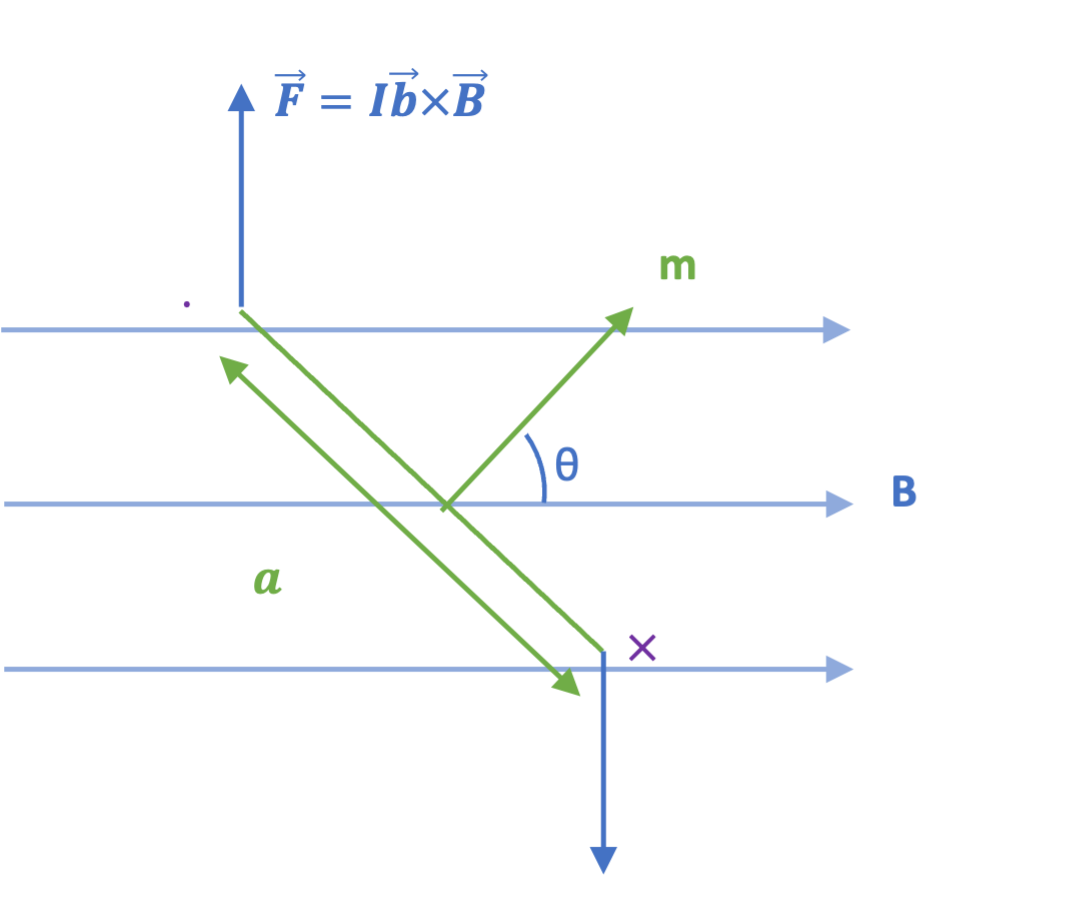
1. 磁偶极子在磁场中所受的力与力矩

图 2：磁偶极子在磁场中所受的力

　　由于 $ \boldsymbol{\mathbf{F}} = I \oint \boldsymbol{\mathbf{l}} \times \boldsymbol{\mathbf{B}} = I (\oint \boldsymbol{\mathbf{l}} ) \times \boldsymbol{\mathbf{B}} = 0$，因此具有环形回路的磁偶极子所受合力始终为零．

　　但是，磁偶极子在磁场中的受合力矩，最终的效果使 $ \boldsymbol{\mathbf{m}} \parallel \boldsymbol{\mathbf{B}} $

\begin{equation} \boldsymbol{\mathbf{M}} = \boldsymbol{\mathbf{m}} \times \boldsymbol{\mathbf{B}} \end{equation}

　　 ------

\begin{equation} \boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \frac{1}{r^3} [3( \boldsymbol{\mathbf{m}} \boldsymbol\cdot \hat{\boldsymbol{\mathbf{r}}} ) \hat{\boldsymbol{\mathbf{r}}} - \boldsymbol{\mathbf{m}} ] \end{equation}