线段树

                     

贡献者： 有机物; addis

　　 线段树（Segment tree）是一种二叉树形的数据结构，用以存储区间或线段，并且可以在 $O(\log N)$ 的时间复杂度查询区间最大值、最小值、总和等属性．

　　 线段树的存储：

　　 线段树除了最后一层节点外是一棵满二叉树，因此可以用堆的存储方式来存储线段树． 具体来说就是开一个一维数组，根节点的编号为 $1$，编号为 $x$ 的结点的左子节点的编号为 $x \times 2$，右子节点的编号为：$x \times 2 + 1$，父节点的编号为 $\left\lfloor\dfrac{x}{2}\right\rfloor$．

　　 因此我们可以用一个结构体来存储线段树，线段树除了最后一层结点外是一棵满二叉树，除了最后一层结点外的结点个数为：$N + \dfrac{N}{2} + \dfrac{N}{4} + \cdots + 2 + 1 = 2N - 1$，最后一层的结点个数最坏情况下是 $2N$ 个结点，所以数组大小应不小于 $4N$ 才能保持不越界．

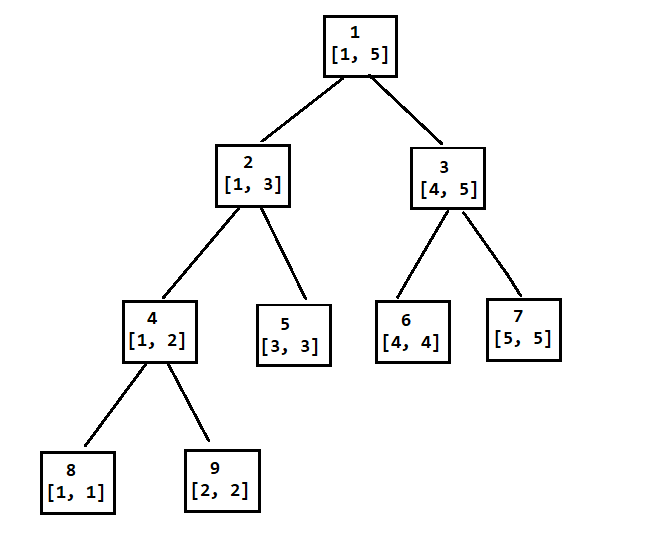
　　 可以看出，线段树的每个结点都代表一个区间，叶结点的区间长度都为 $1$，对于每个区间结点 $[l, r]$，左子结点为 $[l, mid]$，右子结点为 $[mid + 1, r]$，$mid = \left\lfloor\dfrac{l+r}{2}\right\rfloor$．

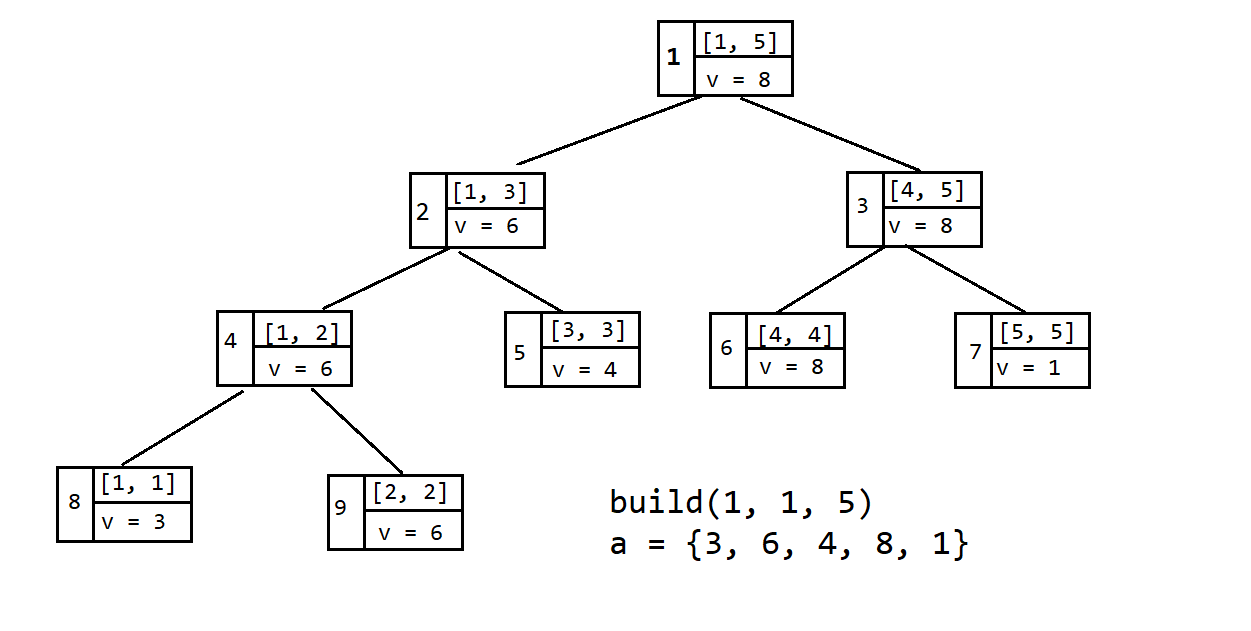
　　 线段树的建树（$\text{build}$）操作：

　　 一般来说，线段树每个结点上存储了很多信息，具体存什么信息得根据具体情况判断，这里以存储区间最大值为例，我们用递归来建树，每个叶结点 $[i, i]$ 保存 $a_i$ 的值，每次递归左子节点和右子节点，最后根据子节点的信息更新当前结点的信息，这一操作称为 $\text{pushup}$ 操作．

struct Node {
    int l, r, v;  // v 代表区间最大值
}tr[4 * N];

void build(int u, int l, int r) 
{
    tr[u] = {l, r};
    
    if (l == r) // 叶节点
    {
        tr[u] = {l, r, a[l]};  // 也可只写 tr[u].v = a[l];
        return;
    }
    
    int mid = l + r >> 1;
    build(u << 1, l, mid);          // 左子节点[l, mid]，编号为：u << 1
    build(u << 1 | 1, mid + 1, r);  // 右子节点[mid + 1, r]，编号为：u << 1 | 1
    pushup(u);
}

build(1, 1, n);   // 调用建树，从根节点开始

　　 线段树的 $\text{pushup}$ 操作：

　　 线段树可以很容易的把左右两个子结点的信息上传到当前结点，所以在记录每个结点 $i$ 的最大值就可以用左子节点 $\mathtt{i < < 1}$ 的最大值和右子节点 $\mathtt{i < < 1|1}$ 的最大值两者取一个最大值就是当前结点 $i$ 的最大值．

void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

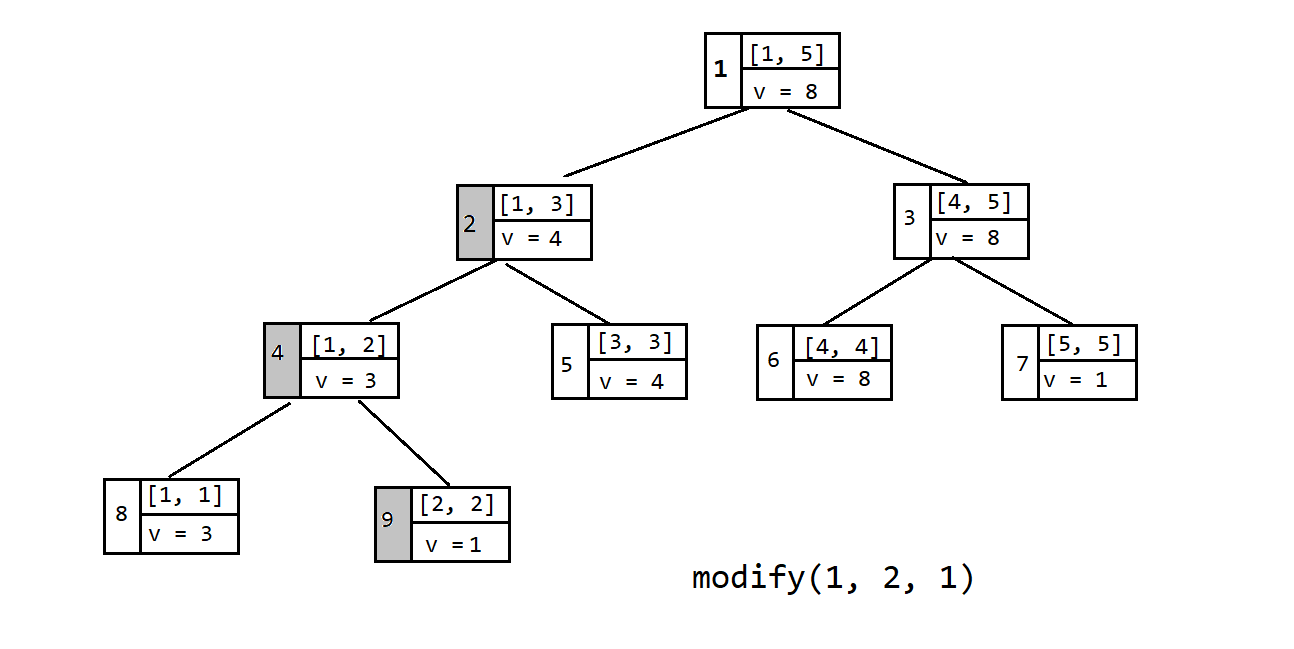
　　 线段树的单点修改（$\text{modify}$）操作：

　　 单点修改操作一般是把 $a[x]$ 的值修改成 $v$，我们从根结点开始，递归左右两个子节点，找到 $[x, x]$ 区间，然后从下往上把对应的父节点保存的最大值进行更新．

void modify(int u, int x, int v)    // 把 a[x] 修改为 v
{
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v;  // 叶节点
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;       // mid 为树中区间的 mid
        if (x <= mid) modify(u << 1, x, v);     // x 属于左半区间
        else modify(u << 1 | 1, x, v);          // x 属于右半区间
        pushup(u);  // 记得更新父节点的值
    }
}

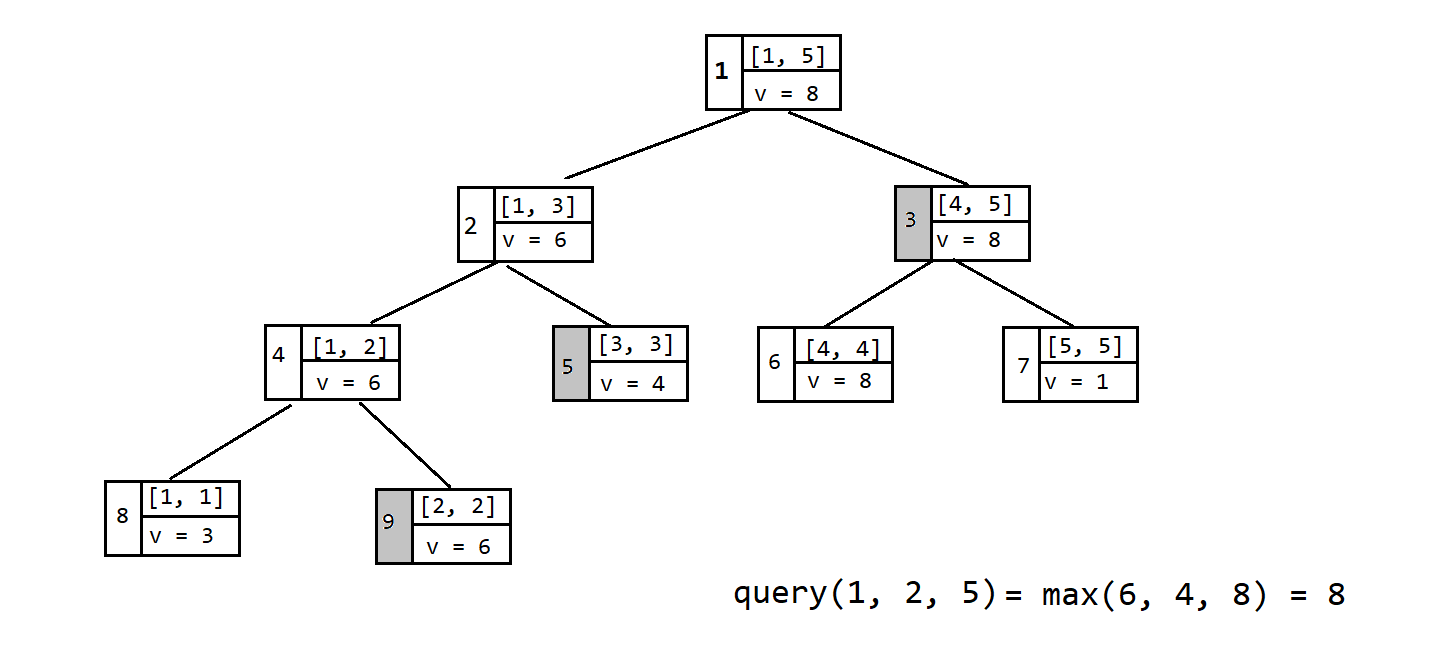
　　 线段树的区间查询（$\text{query}$）操作：

　　 查询操作一般为查询某个区间的某种属性，例如查询区间 $[l. r]$ 内的最大值．我们只需要从根节点开始递归查询，会出现如下几种情况：

1. 查询的区间 $[l, r]$ 完全包含了当前结点的代表区间，则直接返回该区间的最大值，因为没必要再递归查询下去了．
2. 查询的区间 $[l, r]$ 与左子节点有交集，则递归查询左子节点
3. 查询的区间 $[l, r]$ 与右子节点有交集，则递归查询右子节点

　　 查询操作会把询问的区间 $[l, r]$ 分成 $O(\log N)$ 个区间，来简单的证明一下： 在递归每个树上的结点 $[T_l, T_r]$ 时，$mid = \left\lfloor\dfrac{T_l+T_r}{2}\right\rfloor$ 会出现以下几种情况：

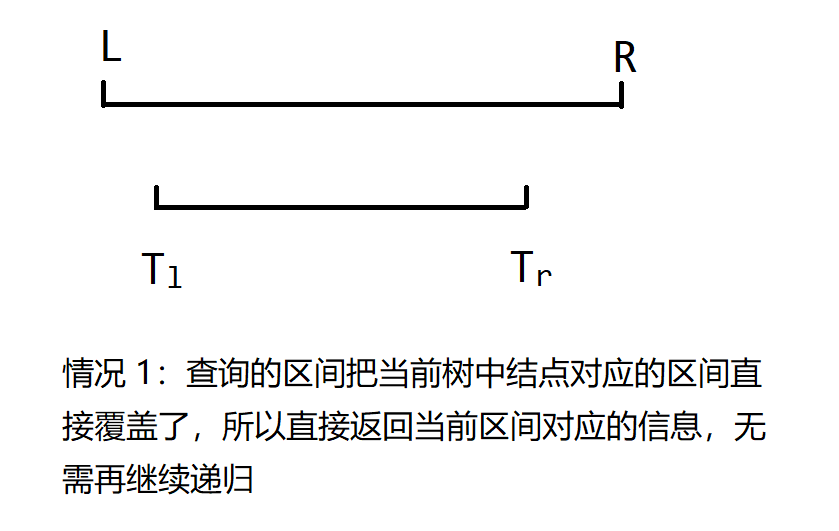
1. $l \leq T_l \leq T_r \leq r$ 即当前树中结点对应的区间完全在查询区间的内部
2. $T_l \leq l \leq T_r \leq r$ 即只有 $l$ 与当前树中结点对应的区间有交集
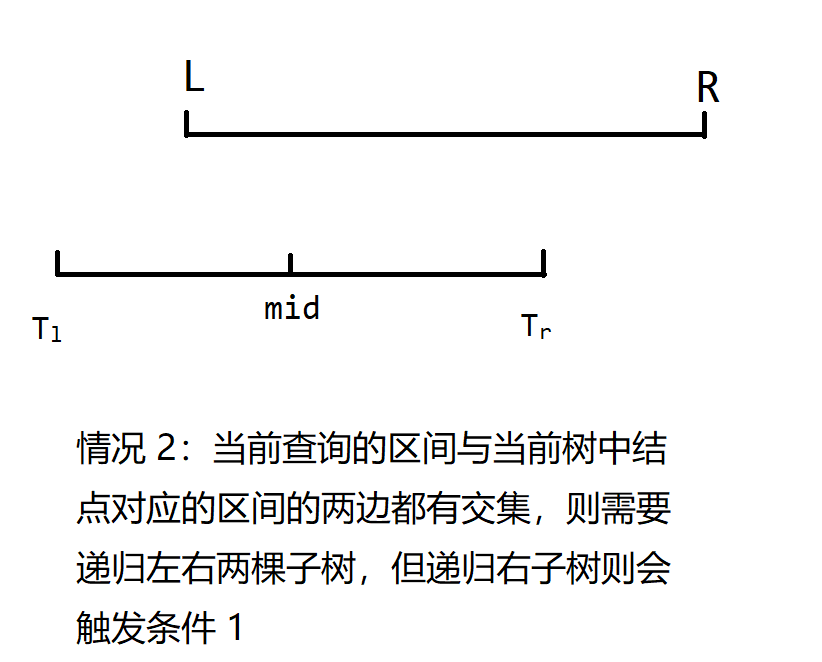
   (1) $l > mid$，$l$ 只与当前树中结点对应的区间的右半部分 $[mid + 1, r]$ 有交集；
   (2) $l \leq mid$，$l$ 与当前树中结点对应的区间的左右两边都有交集，需要递归左右两边，但是递归的右子结点会在递归后直接返回，即触发了情况 $1$.
   
3. $l \leq T_l \leq r \leq T_r$ 即只有 $r$ 与当前树中结点对应的区间有交集，对应情况 $2$．
4. $T_l \leq l \leq r \leq T_r$ 即查询区间完全在当前树中结点对应的区间内部．
   (1) $l > mid$ 时只会递归右子结点；
   (2) $r < mid$ 时只会递归左子节点；
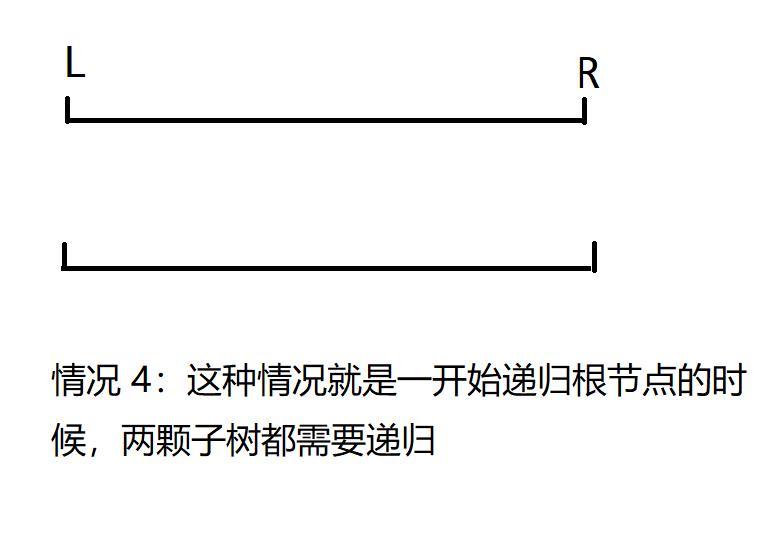
   (3) $l$、$r$ 都与当前树中结点对应的区间有交集，此时需要递归左右子结点．
   

　　 只有 $4(3)$ 这种情况会对线段树的左右两棵子树递归，但这种操作至多发生一次，也就是最开始递归根结点，然后就变成了前三种情况．

int query(int u, int l, int r)
{
    // 完全包含
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;  
    
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if (l <= mid) v = query(u << 1, l, r);
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));
    
    return v;
}

　　 以上就是线段树的基本操作．