Lapack 笔记

贡献者： addis

本词条处于草稿阶段．

预备知识　BLAS 简介

　　 Intel MKL 提供的 Lapack 函数搜索．

　　如果有 Driver 就用尽量用，其次再选 Computational

　　问题类型

linear equations/system of linear equations 线性方程组
nonsymmetric eigenvalue problems 非对称或厄米矩阵本征值问题
symmetric eigenvalue problems 对称或厄米矩阵本征值问题
generalized symmetric-definite eigenvalue problems 广义对称或厄米正定矩阵本征值问题
generalized nonsymmetric eigenvalue problems 广义非对称或厄米正定矩阵本征值问题
linear least square (LLS) problems 线性最小二乘法问题
generalized LLS problems 广义线性最小二乘法问题
singular value decomposition 奇异值分解
cosine-sine decomposition 余弦-正弦分解

　　矩阵类型

对称矩阵
厄米矩阵
正交矩阵
酉矩阵
带对角矩阵
三对角矩阵

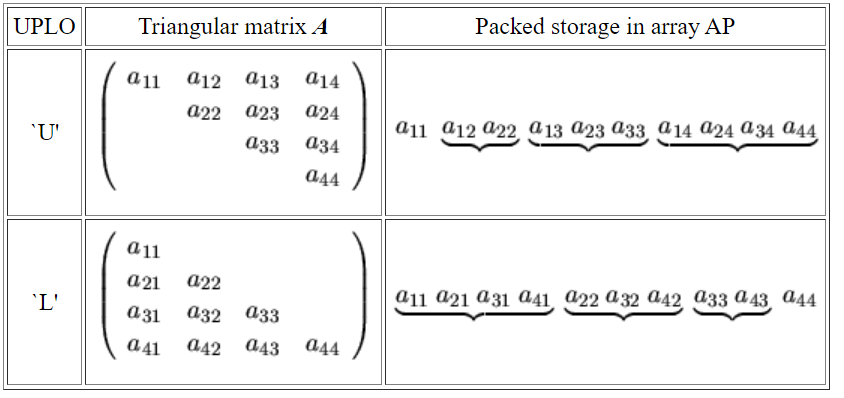
图 1：packed storage 把上半或下半三角矩阵存成一行

　　以下是一些分类搜索结果

1. 线性方程组

Driver - 线性方程组 - 一般矩阵

?gesv 解方矩阵线性方程组，多个 RHS
?gesvx gesv 并提供误差
?gesvxx 用额外循环减小 gesv 的误差
?gbsv gesv 的带对角矩阵版本
?gbsvx gbsv 并提供误差
?gbsvxx 用额外循环减小 gbsv 的误差
?gtsv gesv 的三对角矩阵版本
?gtsvx gtsv 并提供误差

2. 对称本征方程

Driver - 实对称矩阵本征方程 - 所有本征值和本征矢（可选）

?syev 对称矩阵的本征值和本征矢（可选）
?syevd syev 使用 divide and conquer 算法
?spev syev 用 packed storage
?spevd spev 用 packed storage
?sbev syev 用带对角矩阵
?sbevd sbev 用 divide and conquer 算法
?stev syev 使用三对角矩阵

3. 线性最小二乘法

?gels Uses QR or LQ factorization to solve a overdetermined or underdetermined linear system with full rank matrix.
?gelsy Computes the minimum-norm solution to a linear least squares problem using a complete orthogonal factorization of A.
?gelss Computes the minimum-norm solution to a linear least squares problem using the singular value decomposition of A.
?gelsd Computes the minimum-norm solution to a linear least squares problem using the singular value decomposition of A and a divide and conquer method.

致读者：小时百科一直以来坚持所有内容免费，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 10 元，我们一个星期内就能脱离亏损，并保证在接下来的一整年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。