简单的偏振电磁波
贡献者: ACertainUser
- 本词条处于草稿阶段.
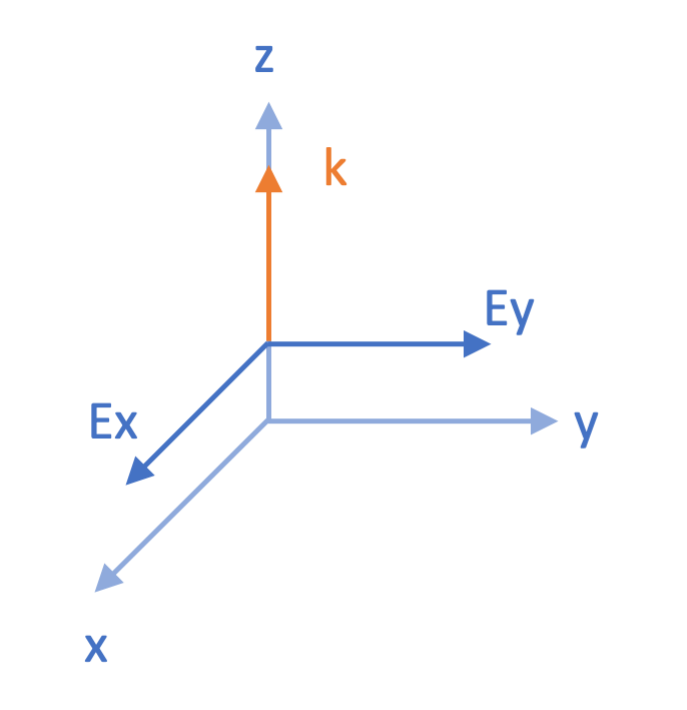
图 1:沿 z 轴传播的电磁波只有 x,y 分量
让我们想象一束沿 $z$ 轴传播的电磁波.由于电磁波是横波,所以 $E_z=0$.为简明起见,我们假定电场 $x,y$ 两个分量的振幅相同,且 $E_x$ 分量的相位因子为 0.2此时,电场的波函数就可以写为
\begin{equation}
\boldsymbol{\mathbf{E}} =
\begin{pmatrix}
E_{0} \cos\left(kz - \omega t\right) \\
E_{0} \cos\left(kz - \omega t+\varphi_{0}\right) \\
0\\
\end{pmatrix}
\end{equation}
根据 $\varphi_0$ 的取值,电磁波也就呈现不同的偏振类型.这让我们联想到利萨茹曲线.
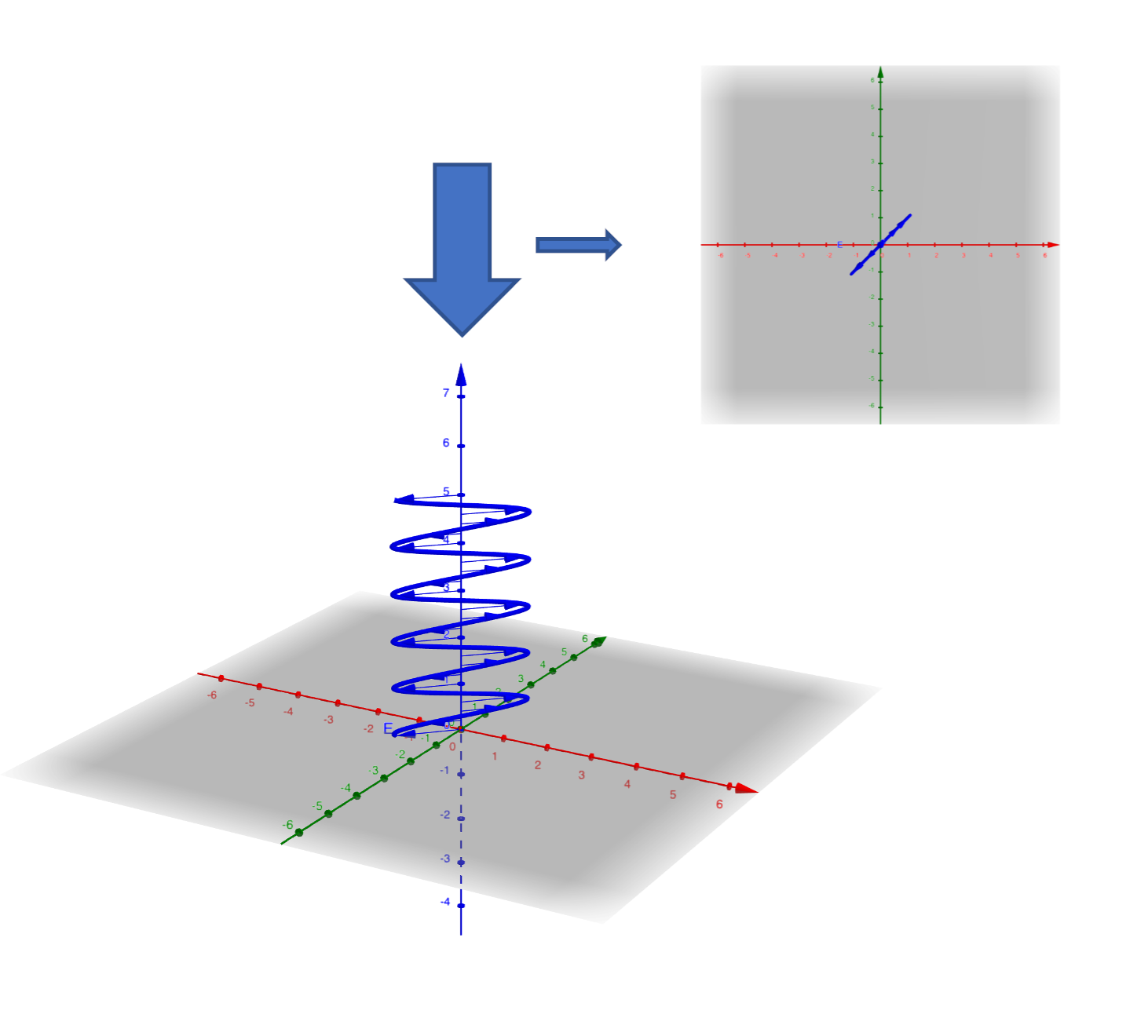
$\varphi_0=n\pi, n=0,\pm1,\pm2,...$:线偏振
图 2:线偏振
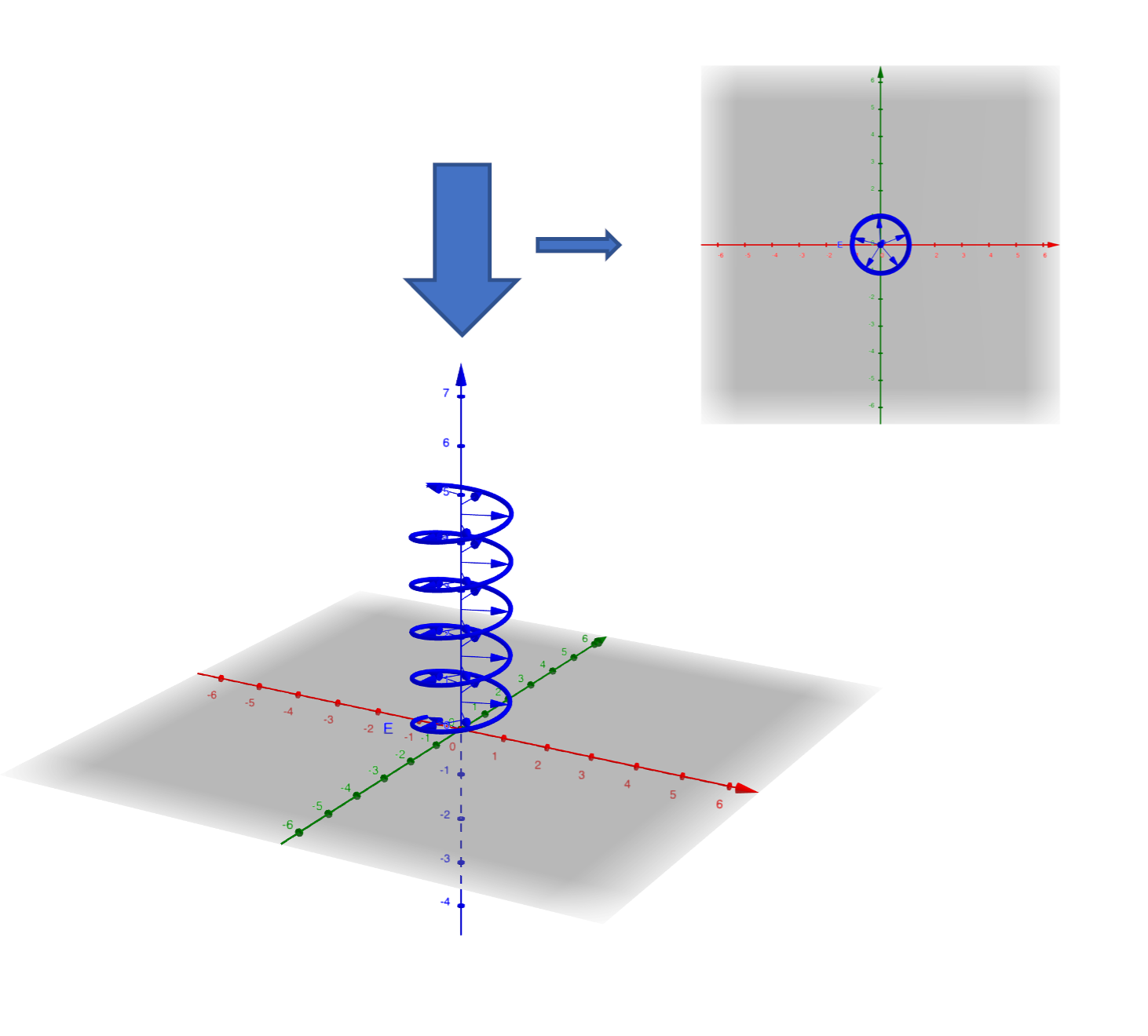
$\varphi_0=\frac{\pi}{2}n, n=\pm1,\pm3,\pm5,...$:圆偏振
图 3:圆偏振,一个可动的模型(站外链接)
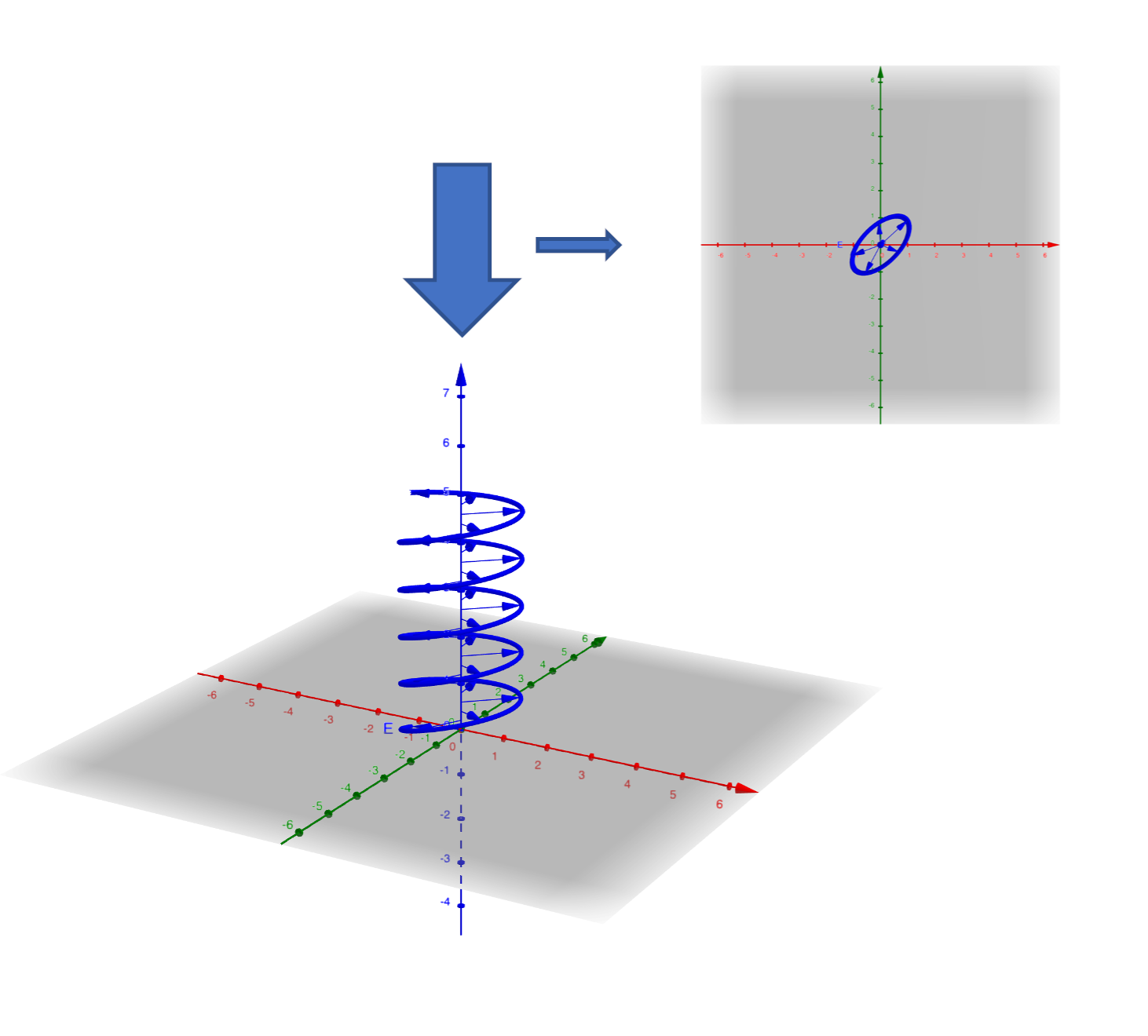
其余情况:椭圆偏振
图 4:椭圆偏振