简单刚体系统的静力学分析
贡献者： ACertainUser
本文简要介绍分析简单平面刚体系统的静力学分析．1
1. 轻绳与轻杆模型
轻绳
拉紧的轻绳只能受拉而不能受压．
拉紧的轻绳向与其相连的刚体提供拉力，但不能提供压力（轻绳不能被压缩）；如果轻绳被拉直，那么轻绳提供的拉力方向总是平行于绳．
轻杆
轻杆可以受压或受拉，同时轻杆提供的力的方向也不一定平行于轻杆．
2. 常见约束条件
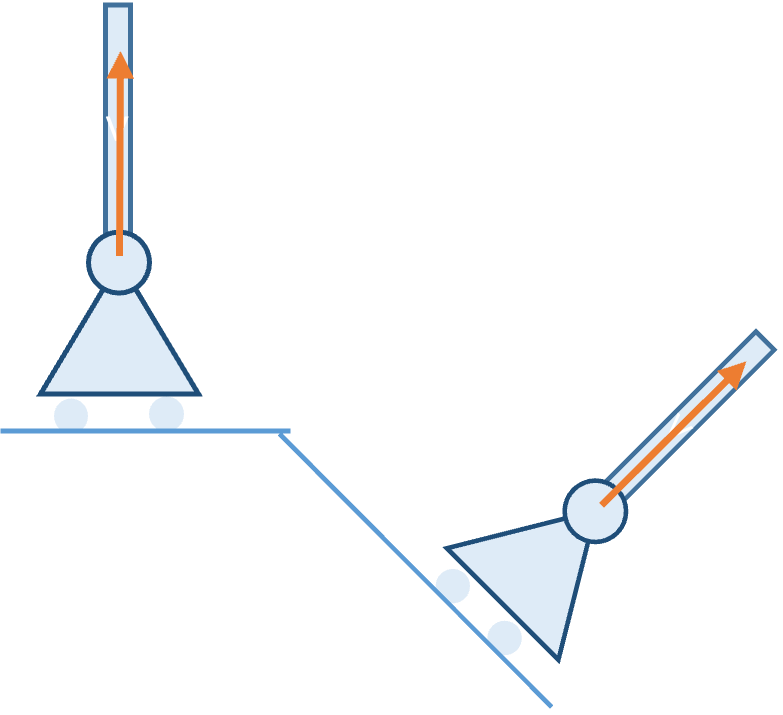
接触面 Surface Constraint
放置于平坦接触面的刚体受一个垂直于公切面的支持力．如果接触面粗糙，还可以提供一个平行于接触面的静摩擦力．
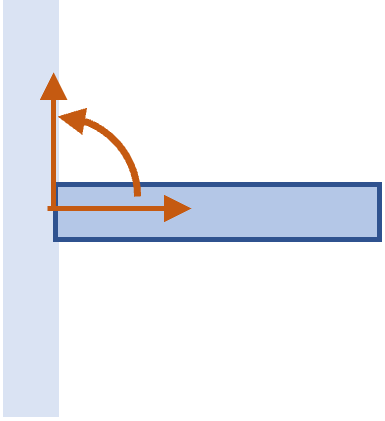
小车模型 Roller Support
小车可以为与其相连的杆提供一个垂直接触面向上的支持力，但是不能提供一个垂直表面向下的拉力；如果接触面是粗糙的，那还能提供一个平行于接触面的静摩擦力．
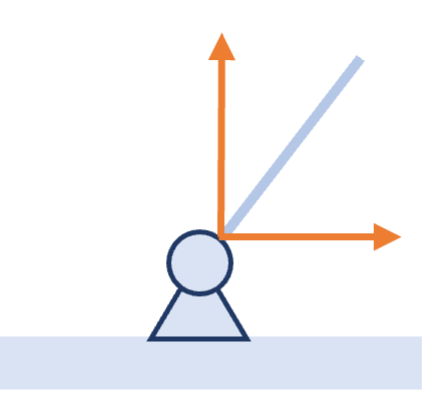
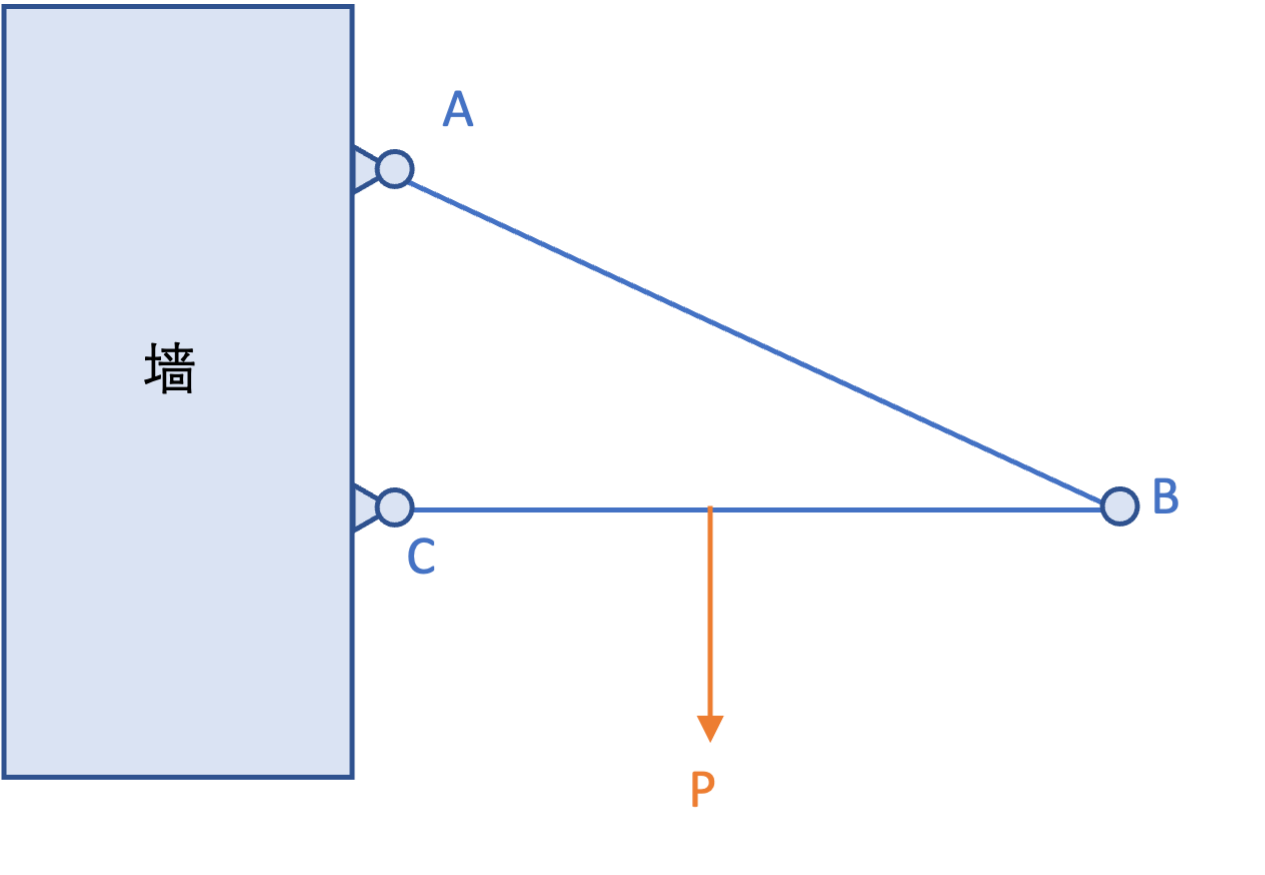
铰链模型 Fixed Hinge
铰链可以为与其相连的杆提供一个任意方向的力，但是不能提供力偶．在初步的受力分析中，力的方向不能确定，因此可以先记为两个互相垂直的分力．
钉子模型 Fixed Rod
杆钉入墙中的部分可以提供一个任意方向的力与一个力偶．同铰链一样，力的方向无法立刻确定，先记为两个互相垂直的分力．
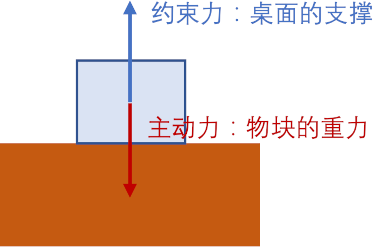
3. 主动力与约束力
先简要定义约束力与主动力：
- 约束力：由于约束条件而产生的力，例如桌面对物体产生的支持力，绳子对物体提供的拉力等．
- 主动力：由于其他外界因素而产生的力，例如重力、外加的压力等．
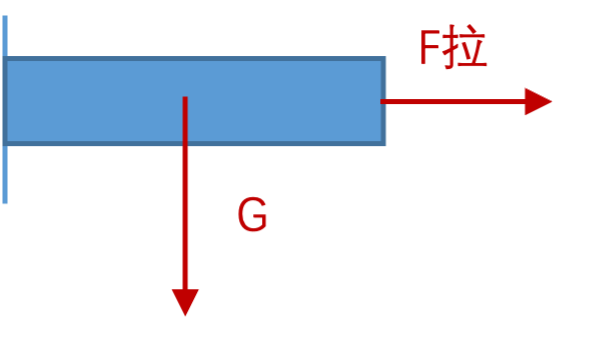
4. 受力分析
总体思路是系统法与隔离法，即先分析系统的整体受力，再逐个分析系统内各个组件的受力．分析系统受力不是一蹴而就，经常是一个反复试错、修正的过程．
- 先把系统视作一个整体，进行受力分析．此时，系统中各刚体之间的约束力是内力，均可被忽略．
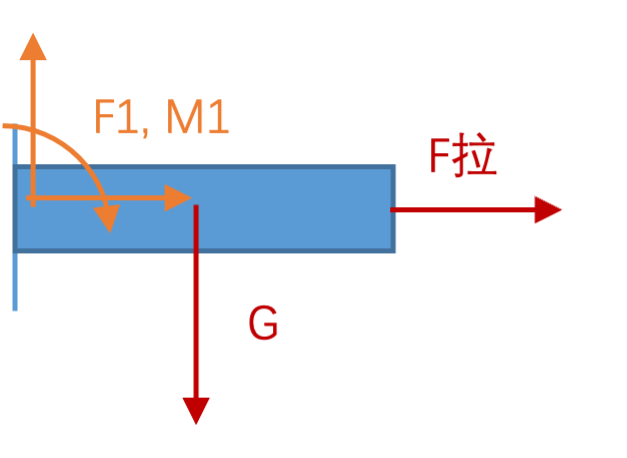
- 随后逐个分析系统内各个组件的受力．一般而言，先分析受到主动力的组件，以及只受两个力的组件（由二力平衡定理立刻得知该两力等大、反向、作用点共线）．
在分析一个组件时，标注主动力，
并根据约束条件标注约束力（注意到，此时系统中其他组件对该组件的约束力不能再被忽视），
最终根据刚体平衡条件计算，并得到各个约束力．
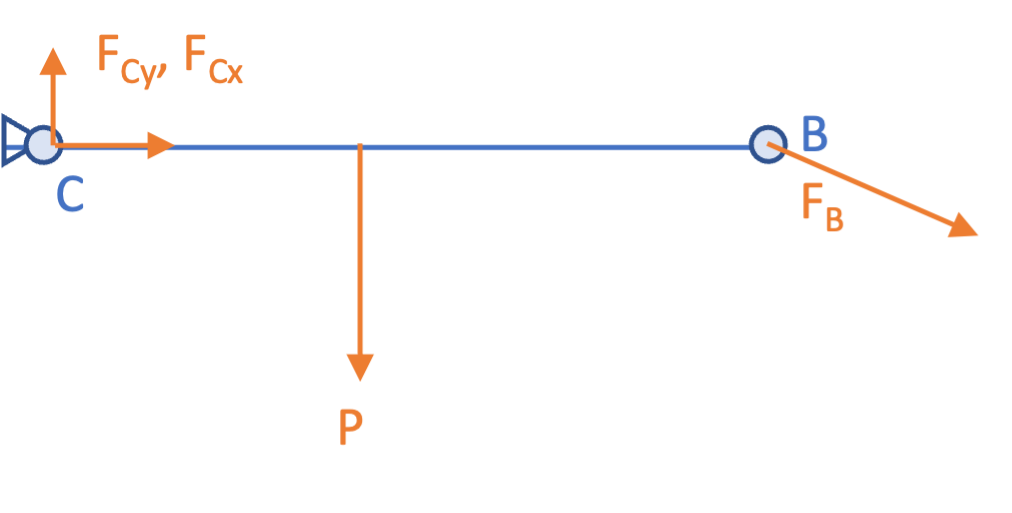
根据牛顿第三定律，若 A 对 B 施加约束力，那么 B 对 A 也会施加一个等大反向的约束力．标注组件的约束力时必须注意到这一点．同时，若 A 对 B 施加的约束力已被确定，那么 B 对 A 施加的约束力也随之确定．
5. 刚体平衡条件
对于一个刚体，处于平衡的条件是合力为 0，且力矩和为 0.2
对于合力，一般把所有力分解至水平与竖直方向，在这两个方向上的合力分别为 0. 力是有方向的，在这种平面情况下，以正负号代表方向．可选取水平向右、垂直向上为正方向．
对于力矩和，一般选取未知力较多的点作为参考点，因为作用点在该点上的未知力关于该点的力矩均为 0．同时，计算力矩时，也是一般把力分解至水平与竖直方向，分别计算力矩．力矩也是有方向的，在这种平面情况下，以正负号代表方向．可使用右手法则确定力矩的正负：拇指放在参考点，四指指向力的方向．拇指向纸面内为正，朝纸面外为负．
例 1 框架结构的受力
如图，杆的重力均不计，分析框架的受力
先分析系统的整体受力．但此时未知力太多，无法得到有价值的信息．
再分析 AB 杆的受力．显然，AB 杆只受两个力（分别由两个铰链提供），根据二力平衡定理，两力等大、反向、作用点共线．
再分析 BC 杆的受力．注意根据牛顿第三定律，B 处力的方向已经可以确定．
最后，根据各组件力的平衡条件列方程组，即可解得 $ \boldsymbol{\mathbf{F}} _A, \boldsymbol{\mathbf{F}} _B, \boldsymbol{\mathbf{F}} _C$．例如，在 BC 杆中，可列出平衡方程：
x 方向合力为 0: $F_{Cx}-P-F_{B} \cos \theta=0$
y 方向合力为 0: $F_{Cy}-P-F_{B}\sin \theta=0$
关于 C 点的力矩和为 0: $P \cdot l_{CP} + F_{By} \cdot l_{CB} = 0$
共有 3 个未知量（$F_{Cx}, F_{Cy}, F_B$）与 3 个方程，原则上可以解出全部未知力．
1. ^ 本文参考了张娟著《理论力学》.本文无协议冲突的部分适用于 CC-BY-SA，否则相应部分遵循原协定．
2. ^ 或许你已经知道，若合力为 0 但力矩和不为 0，那么刚体会开始加速旋转
3. ^ 图片来自网络