贡献者: ACertainUser
1
对于一块材料,我们很容易用截面法分析出材料某一截面上的受力情况;但是,截面法只能告诉我们整个截面的 “总内力”,却不能告诉我们截面上 “具体一点处” 的受力.事实上,在不少情况下,截面各处的受力是不一样的.
1. 微元体与应力
为了更好地处理截面上一处的受力,类似于微积分中 “划分小块体积” 的思想,我们假定材料是由无数小正方形块组成的2,每一小块被称作 “微元体 Element”.这样,材料每一点处的受力就转换为相应处一个微元体的受力.
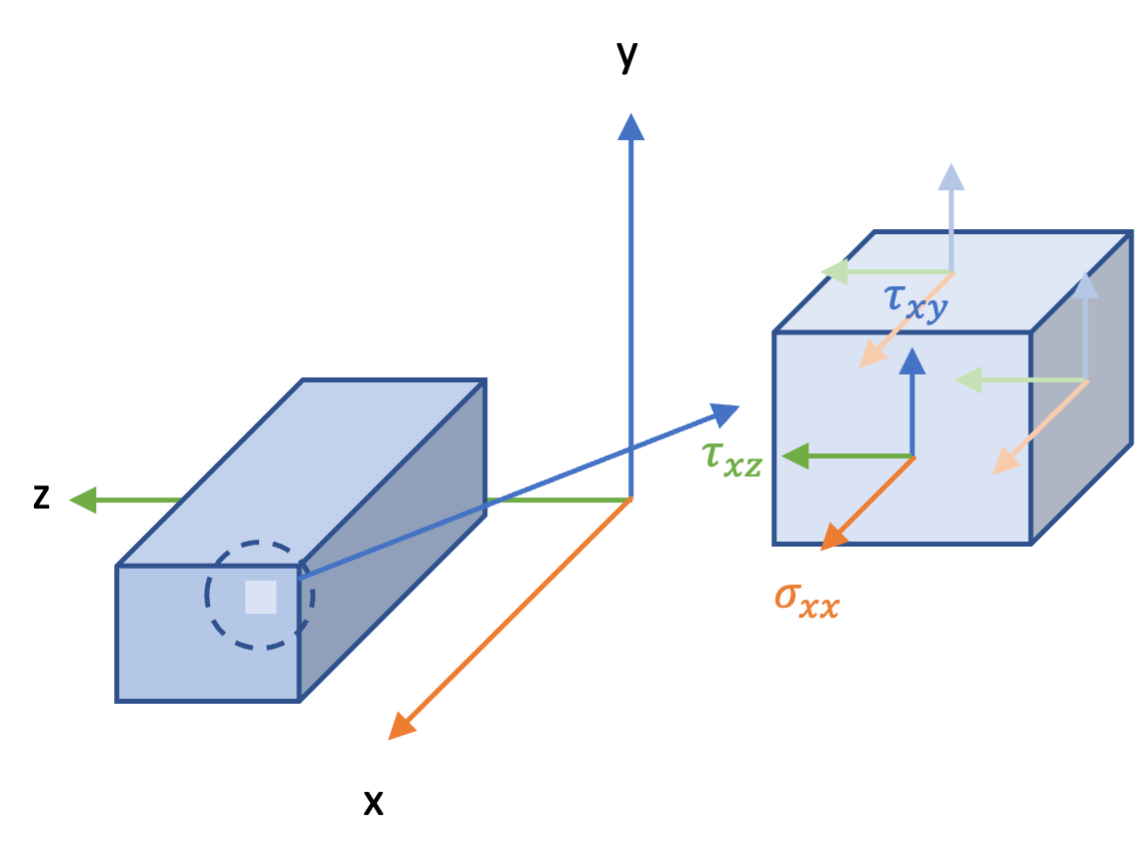
图 1:三维微元体.仿自 P. Beer 的 Mechanics of Materials
应力
为了更好地刻画微元体受力的 “局域性”,类似于密度 $\rho= \frac{\mathrm{d}{m}}{\mathrm{d}{V}} , \,\mathrm{d}{m} = \rho \,\mathrm{d}{V} $ 等概念,我们引入应力的概念.
定义 1 正应力与切应力
在微元体的一个面上,定义垂直于表面的 “力” 为正应力 $\sigma$、平行于表面的 “力” 为切应力 $\tau$.3
正应力:$$\sigma_{ii} = \frac{\mathrm{d}{F_{ii}}}{\mathrm{d}{A}} , \,\mathrm{d}{F} _{ii} = \sigma_{ii} \,\mathrm{d}{A} $$
切应力:$$\tau_{ij}= \frac{\mathrm{d}{F_{ij}}}{\mathrm{d}{A}} , \,\mathrm{d}{F} _{ij} = \tau_{ij} \,\mathrm{d}{A} $$
$ \,\mathrm{d}{F} _{ij}$ 表示微元体这个面上 “分担” 的内力,$ \,\mathrm{d}{A} $ 表示这个微元体这个面的表面积.类似于微积分的思想,当微元体足够小时,微元体表面上不同处的受力大小也趋于一致.
i 表示这个力的作用面的法方向,j 表示这个力的方向4.
三维情况
如图 1 ,微元体的每一个面上可以受 3 个力,包括一个垂直于表面的力与两个平行于表面的力.
看起来,一个微元体上共有 $3\times6=18$ 个力;但考虑到微元体处于静力平衡(,子节 5 ),可以证明事实上一个微元体上只有 6 个相互独立的力.
未完成:补充证明
一个微元体的受力情况可以记为一个三阶矩阵,注意这个矩阵是对称的:
\begin{equation}
\boldsymbol{\mathbf{\sigma}} =
\begin{bmatrix}
\sigma_{xx} & \tau_{xy} & \tau_{xz} \\
\tau_{yx} & \sigma_{yy} & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \sigma_{zz} \\
\end{bmatrix}
\end{equation}
这六个力可以分别选取 $\sigma_{xx}, \sigma_{yy},\sigma_{zz}, \tau_{xy}, \tau_{xz}, \tau_{yz}$.
二维情况
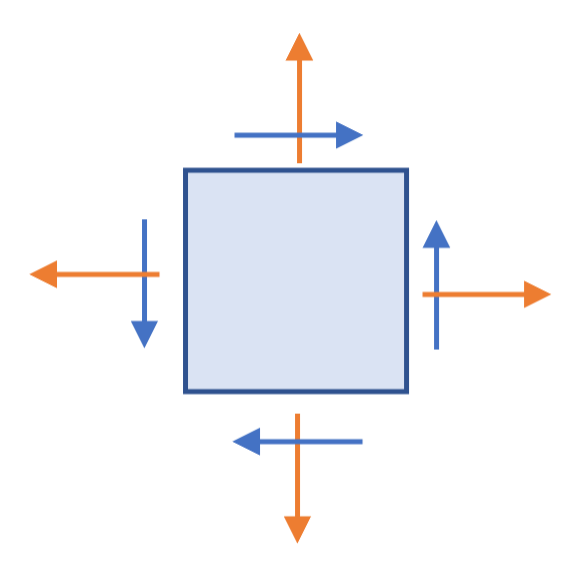
图 2:二维微元体.仿自 P. Beer 的 Mechanics of Materials
二维情况下的微元体更为简单.每一个面上只受一个正应力与一个切应力,共受 $2\times4=8$ 个力,但只有 3 个相互独立的力.此时受力情况可以记为一个二阶矩阵,这个矩阵也是对称的:
\begin{equation}
\boldsymbol{\mathbf{\sigma}} =
\begin{bmatrix}
\sigma_{xx} & \tau_{xy}\\
\tau_{yx} & \sigma_{yy}\\
\end{bmatrix}
\end{equation}
这三个力可以分别选取 $\sigma_{xx}, \sigma_{yy}, \tau_{xy}$.
2. 应力的宏观效果
以上讨论了一个微元体的受力.那微元体上的应力是如何和截面上的总内力联系起来呢?答案是总内力等于各微元体应力的累和.
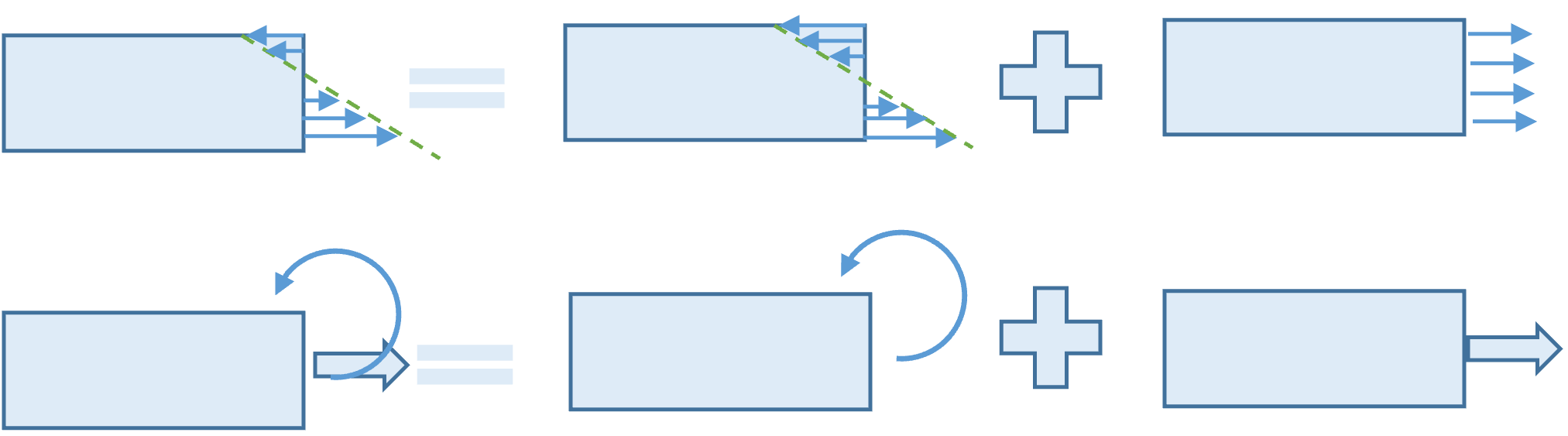
例如,宏观拉力 $F = \iint \sigma_x dA$
图 3:拉力
力偶 $F = \iint y\sigma_x dA$
图 4:力偶
此外,叠加原理依旧适用.假如某截面处的内力既包括拉力、又包括力偶,那某点处的内应力是拉力、力偶单独存在时的内应力之和:
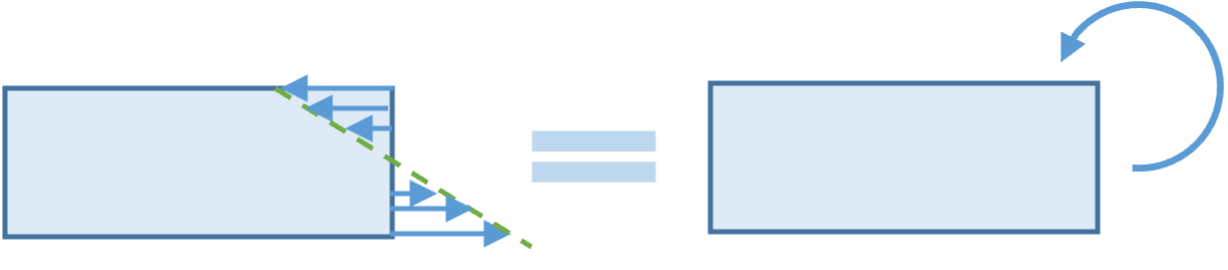
图 5:叠加原理.仿自 P. Beer 的 Mechanics of Materials
那么反过来,我们怎么从截面上的总内力得到各微元体上的应力、即截面上 “具体一点处” 的受力呢?很遗憾,这没有普适的简单方法;但材料力学已经分析了材料的几类常见受力情况,并建立了相应模型,运用这些模型(俗称套公式)就可以计算相应的应力.
1. ^ 本文参考自 P. Beer 的 Mechanics of Materials
2. ^ 这要求材料是 “无限可分” 的,并且每一小块还能维持物理性质不变.这当然是不 “现实”的,不过在初步的学习中,这是一个好的简化近似.
3. ^ 有时不在符号上区分 $\sigma$ 与 $\tau$,并统称为应力
4. ^ 不同作者可能选取不同的约定
致读者: 小时百科一直以来坚持所有内容免费,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 10 元,我们一个星期内就能脱离亏损, 并保证在接下来的一整年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。